DMCommunity Challenge July-2023 deals with a rules-based decisioning problem when not all rules can be satisfied and thus should be considered as preferences. It offers an advanced version of “Miss Manners” (see OpenRules solution) with not equal numbers of males and females at each party. So, the seating arrangement “boy-girl-boy-girl and each guest has someone on the left or right with a common hobby” becomes not a Rule but a Preference. It makes the problem much more difficult to represent and solve especially if we want to find an optimal seating. In this post I will demonstrate how to build the corresponding business decision model using the latest version of OpenRules Rule Solver.

Minimizing Rule Violations . A generic approach to the problems with rules being treated as preferences is an introduction of SOFT and HARD rules. While HARD rules cannot be violated, SOFT rules can. Usually there is a penalty cost associated with such violations and we want to find a decision that minimizes the total rule violation. As an example, you may look at a much simpler but similar problem “Map Coloring with Violations” and how nicely it was solved by OpenRules Solver using soft and hard rules.

For Miss Manners problem with not enough men to be seated between all women, we may assign a gender penalty (say 1) for each violation of the gender seating. Similarly, we may assign a hobby penalty for each hobby violation or consider hobby requirements as hard rules. There are still hard “natural” rules that all guests should occupy different seats. Then we may define the constrained variable “Total Seating Violation” as a sum of all penalty variables and solve an optimization problem that finds such a seating that minimizes “Total Seating Violation”.

Technical Decision Model. Such problems are well investigated in the area of constraint programming: I may refer you to the fundamental work of Ulrich Junker about constraint conflicts and relaxations. Barry O’Sullivan and I presented a good summary at the Business Rules Forum in 2009: “Using Hard and Soft Rules to Define and Solve Optimization Problems“. No wonder the first solution for this problem was quickly provided by Alex Fleischer from IBM who used one of the most powerful constraint solvers CPLEX to present and efficiently solve this problem. It is certainly a nice compact solution based on a specialized constraint programming language OPL. However, it is not easy for a regular programmer (not to mention a business analyst) to understand how Alex defines various constraint violations. My main interest in this challenge was to demonstrate how OpenRules declarative decision modeling approach can be applied to this relatively complex problem and to validate if business analysts would be able to at least understand the provided solution.

Business Decision Model. I built a business decision model for this problem using the latest version of OpenRules Rule Solver: you may see it in one Excel file “MissMannersPreferences.xls” with test cases in the file “MissMannersPreferencesTest.xls“.

The business Glossary for this problem:

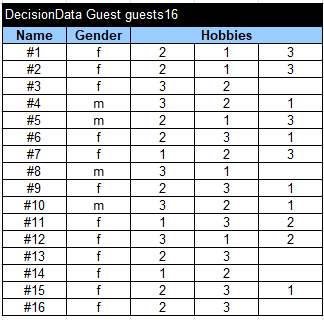
For each Guest we know Name, Gender, and Hobbies. Our goal is to define a Guest’s Seat for all Guests while satisfying Gender and Hobby seating requirements as much as possible.

We will use the standard Rule Solver method “DefineAndSolve” that will utilize these two tables: “Define” for problem definition and “Solve” for problem resolution:

Problem Definition. So, first we need to define our constrained variable (unknown) assuming that seats are numbered from 1 to 16, 32, 64, and 128. The Last Seat is calculated in the above Glossary as a number of elements in the array of Guests. We assume that seats are numbered from 1 to 16, 32, 64, and 128. The Last Seat is calculated in the above Glossary as a number of elements in the array of Guests.

First, we will define Seat Tags for our Party:

We will use these tags to create an array of constrained variables “Seat Variables” for each Guest with the names “{{Name of Guest}}Seat” and the domain from 1 to Last Seat:

All Seat Variables should take different values from 1 to the Last Seat and the First Guest should sit at the First Seat. We may express these constraints in the following table:

Now we need to define Gender and Hobby constraints. First, we will define an intermediate Glossary:

To iterate over all unique pairs of Guests (G1;G2) from the array Guests, we will In the following table

The predefined OpenRules action “ActionNestedLoops” iterates over all elements of the array “Guests” defining the current element as “G1” and then iterates again over the remaining elements of this array defining the current element as “G2”. For each unique pairs of Guests (G1;G2) it will execute rules “SeatingForTwoGuests”:

This table for each pair (G1;G2) will define the string variable “Guest1” as the Name of G1 and the string variable “Guest2” as the Name of G2. Then it will execute decision tables: CreateSeatingViolations and RemoveSymmetry.

This problem is highly symmetrical. To remove symmetries, we will use the following table for each pair (G1;G2):

Table “CreateSeatingViolations”

creates various seating violation constraints in two situations: 1) when guests G1 and G2 have the same gender and 2) when they don’t have common hobbies. This is probably the most complex part of the problem definition that executes the following 3 decision tables:

The first decision table introduces almost natural language expressions to be used to define our seating constraints:

The second table defined all intermediate constraints needed to express all possible constraint violations:

And the third table defines an array “Seating Violations” that contains all constraints that may violate our seating requirements. All these constraints are defined as “SOFT” with the Violation Cost 1:

For example, the last soft constraint states that if “Guest1 not at Last Seat” then “Guest2 not Right of Guest1”. If this constraint is violated the violation cost is 1.

Thus, our objective is to minimize the sum of all Seating Violations for all prohibited situations.

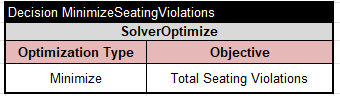
Problem Resolution. First, we define our optimization as the constrained variable “Total Seating Violations”:

Then we execute the standard Rule Solver method that will minimize this objective:

After Rule Solver finds an optimal solution, we want to save all found seats into the array of Guests in the variable Seat of each guest. It can be done using the following table:

This table will also print the solution using the standard ActionPrint.

For large parties (with 32 or more guests), we may stop our search when a certain minimal violation is already achieved. It can be done using this table before calling “MinimizeSeatingViolations”:

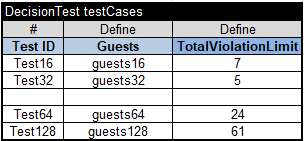
Finally, let’s look at our test cases:

This DecisionTest table refers to DecisionData tables organized like this one for 16 guests:

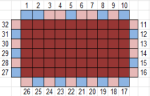
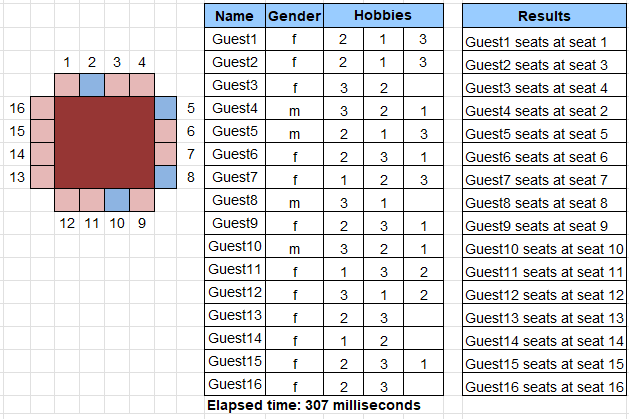
Results. Here are the results for the test case with 16 Guests:

Found a solution with Total Seating Violations[10]. Thu Aug 10 15:46:12 EDT 2023
Found a solution with Total Seating Violations[8]. Thu Aug 10 15:46:12 EDT 2023
Found a solution with Total Seating Violations[7]. Thu Aug 10 15:46:12 EDT 2023

Here are the results for the for test case with 32 Guests:

Found a solution with Total Seating Violations[14]. Thu Aug 10 15:46:12 EDT 2023
Found a solution with Total Seating Violations[13]. Thu Aug 10 15:46:12 EDT 2023
Found a solution with Total Seating Violations[12]. Thu Aug 10 15:46:12 EDT 2023
Found a solution with Total Seating Violations[11]. Thu Aug 10 15:46:12 EDT 2023
Found a solution with Total Seating Violations[10]. Thu Aug 10 15:46:12 EDT 2023
Found a solution with Total Seating Violations[9]. Thu Aug 10 15:46:12 EDT 2023
Found a solution with Total Seating Violations[8]. Thu Aug 10 15:46:12 EDT 2023
Found a solution with Total Seating Violations[7]. Thu Aug 10 15:46:12 EDT 2023
Found a solution with Total Seating Violations[6]. Thu Aug 10 15:46:33 EDT 2023
Found a solution with Total Seating Violations[5]. Thu Aug 10 15:46:33 EDT 2023

The larger sizes of the problem (64 and 128 guests) took more time. So, I decided to limit the search for an optimal result by introducing TotalViolationLimit using the following table:

I defined such a limit directly in the test cases:

It certainly limited the optimality but produced some solutions quickly.

Here are the results for 64 Guests:

Found a solution with Total Seating Violations[32]. Thu Aug 10 16:42:50 EDT 2023
Found a solution with Total Seating Violations[30]. Thu Aug 10 16:42:50 EDT 2023
Found a solution with Total Seating Violations[28]. Thu Aug 10 16:42:51 EDT 2023
Found a solution with Total Seating Violations[26]. Thu Aug 10 16:42:58 EDT 2023
Found a solution with Total Seating Violations[24]. Thu Aug 10 16:43:19 EDT 2023
Guest1 seats at seat 1
Guest2 seats at seat 2
Guest3 seats at seat 3
Guest4 seats at seat 4
Guest5 seats at seat 5
Guest6 seats at seat 6
Guest7 seats at seat 7
Guest8 seats at seat 8
Guest9 seats at seat 9
Guest10 seats at seat 10
Guest11 seats at seat 11
Guest12 seats at seat 12
Guest13 seats at seat 13
Guest14 seats at seat 14
Guest15 seats at seat 15
Guest16 seats at seat 16
Guest17 seats at seat 17
Guest18 seats at seat 18
Guest19 seats at seat 19
Guest20 seats at seat 20
Guest21 seats at seat 21
Guest22 seats at seat 22
Guest23 seats at seat 23
Guest24 seats at seat 24
Guest25 seats at seat 25
Guest26 seats at seat 26
Guest27 seats at seat 27
Guest28 seats at seat 28
Guest29 seats at seat 29
Guest30 seats at seat 30
Guest31 seats at seat 31
Guest32 seats at seat 32
Guest33 seats at seat 33
Guest34 seats at seat 34
Guest35 seats at seat 35
Guest36 seats at seat 36
Guest37 seats at seat 37
Guest38 seats at seat 38
Guest39 seats at seat 39
Guest40 seats at seat 40
Guest41 seats at seat 41
Guest42 seats at seat 42
Guest43 seats at seat 44
Guest44 seats at seat 46
Guest45 seats at seat 48
Guest46 seats at seat 43
Guest47 seats at seat 50
Guest48 seats at seat 45
Guest49 seats at seat 52
Guest50 seats at seat 54
Guest51 seats at seat 47
Guest52 seats at seat 56
Guest53 seats at seat 49
Guest54 seats at seat 51
Guest55 seats at seat 53
Guest56 seats at seat 55
Guest57 seats at seat 57
Guest58 seats at seat 58
Guest59 seats at seat 59
Guest60 seats at seat 60
Guest61 seats at seat 61
Guest62 seats at seat 62
Guest63 seats at seat 63
Guest64 seats at seat 64
Elapsed time: 304,40.81 milliseconds

Here are the results for 128 Guests:

Found a solution with Total Seating Violations[69]. Thu Aug 10 16:56:20 EDT 2023
Found a solution with Total Seating Violations[67]. Thu Aug 10 16:56:20 EDT 2023
Found a solution with Total Seating Violations[65]. Thu Aug 10 16:56:20 EDT 2023
Found a solution with Total Seating Violations[63]. Thu Aug 10 16:56:22 EDT 2023
Found a solution with Total Seating Violations[61]. Thu Aug 10 16:56:23 EDT 2023
Guest1 seats at seat 1
Guest2 seats at seat 2
Guest3 seats at seat 3
Guest4 seats at seat 4
Guest5 seats at seat 5
Guest6 seats at seat 6
Guest7 seats at seat 7
Guest8 seats at seat 8
Guest9 seats at seat 9
Guest10 seats at seat 10
Guest11 seats at seat 11
Guest12 seats at seat 12
Guest13 seats at seat 13
Guest14 seats at seat 14
Guest15 seats at seat 15
Guest16 seats at seat 16
Guest17 seats at seat 17
Guest18 seats at seat 18
Guest19 seats at seat 19
Guest20 seats at seat 20
Guest21 seats at seat 21
Guest22 seats at seat 22
Guest23 seats at seat 23
Guest24 seats at seat 24
Guest25 seats at seat 25
Guest26 seats at seat 26
Guest27 seats at seat 27
Guest28 seats at seat 28
Guest29 seats at seat 29
Guest30 seats at seat 30
Guest31 seats at seat 31
Guest32 seats at seat 32
Guest33 seats at seat 33
Guest34 seats at seat 34
Guest35 seats at seat 35
Guest36 seats at seat 36
Guest37 seats at seat 37
Guest38 seats at seat 38
Guest39 seats at seat 39
Guest40 seats at seat 40
Guest41 seats at seat 41
Guest42 seats at seat 42
Guest43 seats at seat 43
Guest44 seats at seat 44
Guest45 seats at seat 45
Guest46 seats at seat 46
Guest47 seats at seat 47
Guest48 seats at seat 48
Guest49 seats at seat 49
Guest50 seats at seat 50
Guest51 seats at seat 51
Guest52 seats at seat 52
Guest53 seats at seat 53
Guest54 seats at seat 54
Guest55 seats at seat 55
Guest56 seats at seat 56
Guest57 seats at seat 57
Guest58 seats at seat 58
Guest59 seats at seat 59
Guest60 seats at seat 60
Guest61 seats at seat 61
Guest62 seats at seat 62
Guest63 seats at seat 63
Guest64 seats at seat 64
Guest65 seats at seat 65
Guest66 seats at seat 66
Guest67 seats at seat 67
Guest68 seats at seat 68
Guest69 seats at seat 69
Guest70 seats at seat 70
Guest71 seats at seat 71
Guest72 seats at seat 72
Guest73 seats at seat 73
Guest74 seats at seat 74
Guest75 seats at seat 75
Guest76 seats at seat 76
Guest77 seats at seat 77
Guest78 seats at seat 78
Guest79 seats at seat 79
Guest80 seats at seat 80
Guest81 seats at seat 81
Guest82 seats at seat 82
Guest83 seats at seat 83
Guest84 seats at seat 84
Guest85 seats at seat 85
Guest86 seats at seat 86
Guest87 seats at seat 87
Guest88 seats at seat 88
Guest89 seats at seat 89
Guest90 seats at seat 90
Guest91 seats at seat 91
Guest92 seats at seat 92
Guest93 seats at seat 93
Guest94 seats at seat 94
Guest95 seats at seat 95
Guest96 seats at seat 96
Guest97 seats at seat 97
Guest98 seats at seat 98
Guest99 seats at seat 99
Guest100 seats at seat 100
Guest101 seats at seat 101
Guest102 seats at seat 102
Guest103 seats at seat 103
Guest104 seats at seat 104
Guest105 seats at seat 105
Guest106 seats at seat 106
Guest107 seats at seat 107
Guest108 seats at seat 108
Guest109 seats at seat 109
Guest110 seats at seat 110
Guest111 seats at seat 111
Guest112 seats at seat 112
Guest113 seats at seat 113
Guest114 seats at seat 114
Guest115 seats at seat 116
Guest116 seats at seat 118
Guest117 seats at seat 115
Guest118 seats at seat 117
Guest119 seats at seat 120
Guest120 seats at seat 122
Guest121 seats at seat 119
Guest122 seats at seat 124
Guest123 seats at seat 126
Guest124 seats at seat 121
Guest125 seats at seat 123
Guest126 seats at seat 125
Guest127 seats at seat 127
Guest128 seats at seat 128
Elapsed time: 69,694.27 milliseconds

THE END