This problem used to be one of the popular benchmarks for rule engines 20 years ago. And now DMCommunity.org brings it back to see how modern decision engines can represent and solve this problem today. I will demonstrate it in this post with the latest OpenRules Rule Solver.

Problem Description. Miss Manners is throwing a party and being a good host, she wants to arrange good seating. She wants to seat the guests in a boy-girl-boy-girl arrangement so that each guest will have someone on the left or right that has a common hobby. Our decision model needs to help Miss Manners to do it for parties with 16, 32, 64, and 128 guests described in the Excel file that you may download from here.

This is a typical constraint satisfaction problem which could be easily represented and resolved by any Constraint Solver. No wonder DMCommunity quickly received a submission based on IBM Constrained Solver CPLEX. I also quickly created a similar solution using OpenRules with Java Solver. Both these solutions are very efficient and compact but both of them require knowledge of the corresponding programming or specialized languages and hardly could be understood by business analysts.

Below I will show how to represent and solve this problem using the latest OpenRules Rule Solver.

Problem Definition. Let’s start with the provided test data for the party of 16 guests converted to the OpenRules format in Excel file Test.xls:

Here is the corresponding business Glossary:

Thus, for each Guest we know Name, Gender, and Hobbies. Our goal is to define a Guest’s Seat for all Guests while satisfying Gender and Hobby rules (constraints).

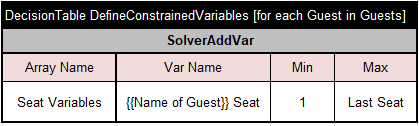
We will assume that seats are numbered from 1 to 16, 32, 64, and 128. The Last Seat is calculated in the above Glossary as a number of elements in the array of Guests. For each Guest, we will create unknown decision variables with names “{{Name of Guest}} Seat” (e.g. “1 Seat”, “2 Seat”, etc.) that can take values from 1 to Last Seat. We call these unknown variables “Solver’s variables”. Using Rule Solver, we can create these variables and put them into an array “Seat Variables” using the following table:

Now we may define all Gender and Hobby rules by posting the proper constraints on these yet unknown decision variables, and then use a standard search strategy to find the proper seats.

First of all, all Seat Variable should take different values from 1 to Last Seat, and we may express this constraint in the following table:

We also may assume the the first guest is always sitting at the first seat as all other decision will be simply symmetrical. We may achieve this by using this table:

To post Gender and Hobby constraints we need to consider all possible pairs of Guests (G1;G2) and state that G1 and G2 should have opposite genders and at least one common hobby. We can do it by posting incompatibility constraints (“DontSeatTogether”) for each pair of different guests G1 and G2 if they have the same Gender or (!) their Hobbies do not intersect. Here is the proper OpenRules table with two nested loops over the same array Guests:

Note that we implemented the above “or” by using two different rules. In both situations we will execute the same Action “DontSeatTogether”. This action is supposed to post the following IT-THEN constraints that would not allow Guest 1 and Guset2 to seat next to each other:

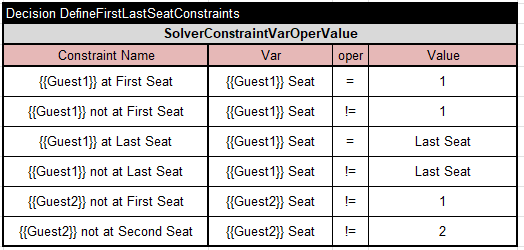
Here {{Guest1}} and {{Guest2}} will be replaced by the actual names of Guest1 or Guest2. We still need to define the constraints like “{{Guest1} at First Seat” and others. It can be done in the following tables:

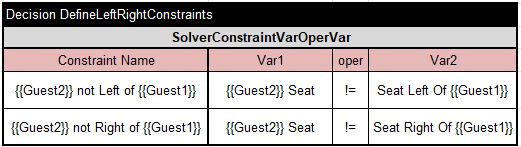
We still need to define Solver’s expressions for “Seat Left Of {{Guest1}}” and “Seat Right Of {{Guest1}}”. It can be done in the following table:

And finally, the action “DontSeatTogether” will execute all these tables for each pair of Guest1 and Guest2:

To complete our Problem Definition, we may use the following table:

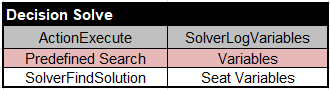
Problem Resolution. We may rely on the predefined search strategy “SolverFindSolution” supported by Rule Solver. We also may print all found values for Seat Variables using the action “SolveLogVariables”:

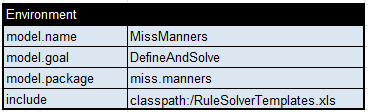
Main Decision. The will rely on the default method “DefineAndSolver” to invoke both tables “Define” and “Solve” as defined by the property “model.goal” in the Environment table:

Here is the automatically generated Decision Diagram:

As you can see, all decision modeling efforts were on problem definition and we don’t have to worry about problem resolution.

Execution Results. Running this decision model produced the following results:

Party of 16 Guests:

1 Seat[1] 2 Seat[2] 3 Seat[3] 4 Seat[5] 5 Seat[7] 6 Seat[9] 7 Seat[4] 8 Seat[11] 9 Seat[13] 10 Seat[15] 11 Seat[6] 12 Seat[8] 13 Seat[10] 14 Seat[12] 15 Seat[14] 16 Seat[16]

Party of 32 Guests:

dave Seat[1] doug Seat[3] jane Seat[2] kate Seat[4] scott Seat[5] sue Seat[6] ann Seat[8] john Seat[7] chuck Seat[9] hope Seat[10] jill Seat[12] dan Seat[11] carol Seat[14] alex Seat[13] pam Seat[16] tim Seat[15]

d Seat[17] e Seat[19] f Seat[18] g Seat[20] h Seat[21] i Seat[22] j Seat[24] k Seat[23] l Seat[25] m Seat[26] n Seat[28] o Seat[27] p Seat[30] q Seat[29] r Seat[32] s Seat[31]

Party of 64 Guests:

1 Seat[1] 2 Seat[2] 3 Seat[3] 4 Seat[5] 5 Seat[7] 6 Seat[9] 7 Seat[4] 8 Seat[11] 9 Seat[13] 10 Seat[15] 11 Seat[17] 12 Seat[6] 13 Seat[19] 14 Seat[21] 15 Seat[23] 16 Seat[8] 17 Seat[10] 18 Seat[25] 19 Seat[12] 20 Seat[14] 21 Seat[27] 22 Seat[29]

23 Seat[16] 24 Seat[18] 25 Seat[20] 26 Seat[31] 27 Seat[22] 28 Seat[33] 29 Seat[24] 30 Seat[26] 31 Seat[35] 32 Seat[37] 33 Seat[39] 34 Seat[28] 35 Seat[30] 36 Seat[41] 37 Seat[43] 38 Seat[32] 39 Seat[45] 40 Seat[34] 41 Seat[47] 42 Seat[49]

43 Seat[51] 44 Seat[53] 45 Seat[55] 46 Seat[36] 47 Seat[57] 48 Seat[38] 49 Seat[59] 50 Seat[61] 51 Seat[40] 52 Seat[63] 53 Seat[42] 54 Seat[44] 55 Seat[46] 56 Seat[48] 57 Seat[50] 58 Seat[52] 59 Seat[54] 60 Seat[56] 61 Seat[58] 62 Seat[60] 63 Seat[62] 64 Seat[64]

Party of 128 Guests:

1 Seat[1] 2 Seat[2] 3 Seat[4] 4 Seat[3] 5 Seat[5] 6 Seat[6] 7 Seat[8] 8 Seat[7] 9 Seat[9] 10 Seat[11] 11 Seat[13] 12 Seat[10] 13 Seat[12] 14 Seat[15] 15 Seat[17] 16 Seat[19] 17 Seat[21] 18 Seat[14] 19 Seat[23] 20 Seat[25] 21 Seat[27]

22 Seat[29] 23 Seat[16] 24 Seat[18] 25 Seat[31] 26 Seat[33] 27 Seat[35] 28 Seat[20] 29 Seat[22] 30 Seat[37] 31 Seat[39] 32 Seat[24] 33 Seat[28] 34 Seat[41] 35 Seat[26] 36 Seat[43] 37 Seat[30] 38 Seat[32] 39 Seat[45] 40 Seat[47] 41 Seat[40] 42 Seat[49] 43 Seat[51]

44 Seat[34] 45 Seat[53] 46 Seat[55] 47 Seat[57] 48 Seat[36] 49 Seat[59] 50 Seat[61] 51 Seat[63] 52 Seat[38] 53 Seat[42] 54 Seat[60] 55 Seat[65] 56 Seat[67] 57 Seat[44] 58 Seat[69] 59 Seat[46] 60 Seat[48] 61 Seat[71] 62 Seat[50] 63 Seat[52] 64 Seat[54] 65 Seat[73]

66 Seat[56] 67 Seat[58] 68 Seat[75] 69 Seat[77] 70 Seat[62] 71 Seat[79] 72 Seat[81] 73 Seat[64] 74 Seat[66] 75 Seat[68] 76 Seat[70] 77 Seat[83] 78 Seat[85] 79 Seat[72] 80 Seat[87] 81 Seat[89] 82 Seat[91] 83 Seat[74] 84 Seat[93] 85 Seat[76] 86 Seat[95] 87 Seat[97]

88 Seat[99] 89 Seat[78] 90 Seat[101] 91 Seat[80] 92 Seat[82] 93 Seat[84] 94 Seat[86] 95 Seat[88] 96 Seat[103] 97 Seat[90] 98 Seat[105] 99 Seat[98] 100 Seat[107] 101 Seat[92] 102 Seat[94] 103 Seat[109] 104 Seat[111] 105 Seat[96] 106 Seat[100] 107 Seat[102] 108 Seat[104]

109 Seat[108] 110 Seat[113] 111 Seat[110] 112 Seat[106] 113 Seat[112] 114 Seat[115] 115 Seat[117] 116 Seat[119] 117 Seat[114] 118 Seat[116] 119 Seat[121] 120 Seat[123] 121 Seat[118] 122 Seat[125] 123 Seat[127] 124 Seat[120] 125 Seat[122] 126 Seat[124] 127 Seat[126] 128 Seat[128]

Performance. While performance is already good (130 milliseconds for the party of 16 and 20 seconds for the party of 128) we may essentially improve it by modifying Problem Definition without touching Problem Resolution. This problem has a lot of symmetrical solutions for guests with the same genders and hobbies. To break such symmetry we may add additional constraints for such guests:

As the standard loops in the above table “PostIncompatibilityConstraints” do not support indexes (yet!), we may replace this table with two tables utilizing simple nested loops in Java:

It produces the same results but much faster:

Party Size	Execution Time (milliseconds)	Execution Time (milliseconds) After Removing Symmetry
16	110	111
32	142	73
64	955	304
128	16.411	4,290

THE END