Everybody is familiar with Sudoku: you need to fill a 9×9 grid in a such way that each column, each row, and each of the nine 3×3 boxes (also called blocks) contains the digits from 1 to 9, only one time each. In this post I’ll show how easy to build a Sudoku decision model using the latest OpenRules Rule Solver.

First, let’s define a few test instances of the game in simple Excel tables assuming that zeros represent unknown cells:

We may choose these and other games instances using a regular OpenRules table that defines test-cases:

Here MatrixInt is a predefined OpenRules type and “Game Instance” is a variable defined in this simple Glossary:

The default main decision “DefineAndSolve” uses these two sub-decisions:

Let’s look at all these steps:

Step 1 “CreateMatrix”. Rule Solver has a Java method

VarMatrix createVarMatrix(String matrixName, int min, int max, int rows, int columns)

that can create a matrix of size “rows x columns” containing constrained variables with domain [min..max]. The following Excel table of the type “Method” uses a Java snippet to create a Sudoku 9×9 matrix and initialize it with the selected Game Instance:

Step 2 “CONSTRAINTS”. The most important second step “DefineSudokuConstraints” effectively utilizes the predefined column type “SolverAllDiff” which ensures that no two variables inside the provided list can have the same value (All Different):

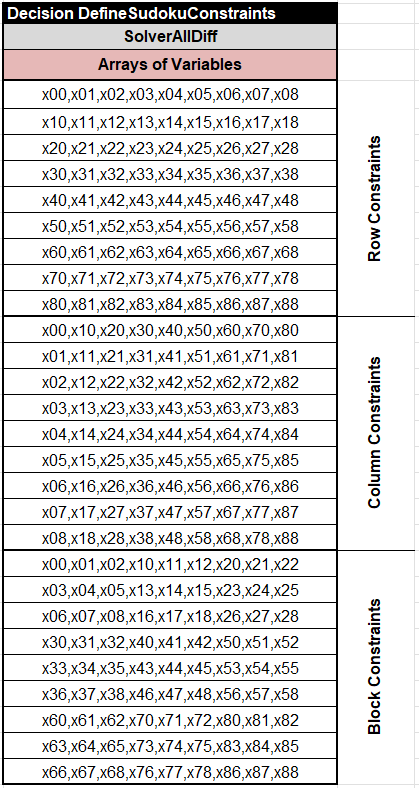
Hope you will find these constraints to be highly intuitive.

Step 3 “SEARCH”. To solve the problem we don’t need to do anything and simply call a predefined Rule Solver search method “SolverFindSolution“.

Step 4 “PRINT”. The last step prints solution using Java snippet: decision.log(“SOLUTION:\n” + ${Matrix});

It will print a found solution, e.g. this is a solution for the test-instance:

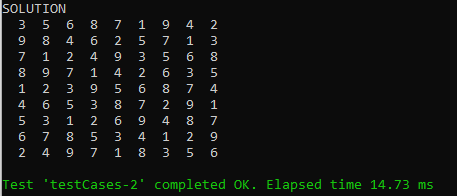
I hope you will find this decision model be quite intuitive. More importantly it can find a solution for a Sudoku problem of any complexity within milliseconds. By modifying the decision table “DefineSudokuConstraints” we may similarly implement Sudoku variations.

THE END